Definición de límite

El límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor. En cálculo (especialmente en análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación, integración, entre otros.

Límite de una función

Visualización de los parámetros utilizados en la definición de límite.

Definición rigurosa

Informalmente, se dice que el límite de la función f(x) es L cuando x tiende a p , y se escribe

$lim_{xto p} , , f(x) = L$

si se puede encontrar un x suficientemente cerca de p tal que el valor de f(x) sea próximo a L. Formalmente, utilizando términos lógico-matemáticos:

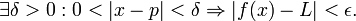
$f(x) to L Longleftrightarrowforall epsilon > 0$ $exists delta > 0 : 0<|x-p|<delta Rightarrow |f(x)-L|<epsilon.$

Esta definición se denomina frecuentemente definición épsilon-delta de límite, y se lee como:

"El límite de la función f(x), cuando x tiende a p, es L".

Límites notables

Como ejemplo de límites notables tenemos los siguientes límites de funciones, que proveen resultados muy interesantes.

${lim_{x to infty} left (1+ frac {1}{x} right )^x } =, e$ (número e)

${lim_{x to 0} left (frac {operatorname{sen,} x}{x} right )} =, 1$ (al igual que su recíproca)
${lim_{x to 0} left (frac {tan x}{x} right )} =, 1$ (al igual que su recíproca)

Demostración

Para demostrar, por ejemplo, el segundo de estos límites, se utilizará la inecuación sen(x) < x < tan(x) en el intervalo (0,π/2), que relaciona x con las funciones seno y tangente. Luego dividimos por sen(x), obteniendo:

$1 < frac{x}{operatorname{sen,}(x)} < frac{1}{cos(x)}$

Elevando los términos de la inecuación a -1:

$cos(x) < frac{operatorname{sen,} x}{x} < 1$

Calculando el límite cuando x tiende a 0:

$lim_{xto 0} cos(x) < lim_{xto 0} frac{operatorname{sen,}(x)}{x} < lim_{xto 0} 1$

Lo que es igual a:

$1 < frac{operatorname{sen,}(x)}{x} < 1$

Aplicando el teorema del sándwich, el límite se ve forzado a valer 1:

$lim_{xto 0}frac{operatorname{sen,}(x)}{x}=1$

El tercero de los límites se demuestra utilizando las propiedades de los límites y el valor obtenido en el límite anterior. O sea:

${lim_{x to 0} left (frac {tan x}{x} right )} = {lim_{x to 0} left (frac {operatorname{sen,} x}{x} right )} cdot lim_{x to 0} frac{1}{cos(x)}= 1 cdot 1 = 1$

El límite que obtiene el número e se demuestra de manera análoga, desarrollando el binomio de Newton y aplicando el límite cuando x tiende a infinito.

Límite de una sucesión

$a_{n} = begin{cases} 16 & mbox{si } n = 0 cfrac{a_{n-1}}{2} & mbox{si } n > 0 end{cases}$

La definición del límite matemático en el caso de una sucesión es muy parecida a la definición del límite de una función cuando $x$ tiende a $infty$ . Decimos que la sucesión $a n$ tiende hasta su límite $a$ , o que converge o es convergente (a $a$ ), lo que denotamos como:

$lim_{ntoinfty}a_n = a$

si podemos encontrar un número $N$ tal que todos los términos de la sucesión a $a$ cuando $n$ crece sin cota. Formalmente:

$a_n to a Leftrightarrow$ $forallepsilon>0, exists N>0 : forall nge N, |a_n - a|<epsilon$

Propiedades de los límites

Generales

Los límites, como otros entes matemáticos, cumplen las siguientes propiedades generales, que son usadas muchas veces para simplificar el cálculo de los mismos.

$lim_{x to a} x = , a ,$

Límite por un escalar.

$lim_{x to a} kf(x) =, klim_{x to a} f(x),$ donde k es un multiplicador escalar.

Límite de una suma.

$lim_{x to a} (f(x) + g(x)) =, lim_{x to a} f(x) + lim_{x to a} g(x),$

Límite de una resta.

$lim_{x to a} (f(x) - g(x)) =, lim_{x to a} f(x) - lim_{x to a} g(x),$

Límite de una multiplicación.

$lim_{x to a} (f(x) cdot g(x)) =, lim_{x to a} f(x) cdot lim_{x to a} g(x),$

Límite de una división.

$underset {x to a} {lim} ; frac {f(x)}{g(x)} = frac {underset {x to a} {lim} ; f(x)} {underset {x to a} {lim} ; g(x)} quad mathrm{si} lim_{x to a} g(x) ne 0$

Indeterminaciones

Hay límites que evaluándolos directamente, se obtiene alguna de las siguientes expresiones:

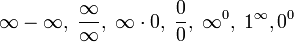
$infty - infty, ; frac{infty}{infty}, ; infty cdot 0 , ; frac{0}{0}, ; infty ^0, ; 1^infty,0^0 ,$

A estas expresiones se les denomina indeterminaciones, ya que, a simple vista, no está claro cual puede ser el límite (si es que existe). En algunos casos, simplificando las expresiones u obteniendo expresiones equivalentes a las iniciales se puede resolver la indeterminación y calcular el límite. En otros casos, se requerirá el uso de otras herramientas más potentes como pueden ser desigualdades o la regla de L'Hopital.

Un ejemplo de indeterminación del tipo $textstyle frac{0}{0}$ es la que se da en estos tres casos, y en cada caso (tras simplificar), se obtiene un límite distinto :

$lim_{trightarrow 0}frac{t}{t^2}=frac{0}{0} quad xrightarrow[mathrm{simplificando}]{} quad lim_{trightarrow 0}frac{1}{t} = infty$

$lim_{trightarrow 0}frac{t}{t}=frac{0}{0} quad xrightarrow[mathrm{simplificando}]{} quad lim_{trightarrow 0} 1 =1$

$lim_{trightarrow 0}frac{t^2}{t}=frac{0}{0} quad xrightarrow[mathrm{simplificando}]{} quad lim_{trightarrow 0} {t} = 0$

arriba